发表于

实现：github

前言

本文介绍了使用GO语言实现Selpg这样一个程序的过程，总体参考了开发Linux命令行实用程序这篇文章，它讲的是使用C语言实现Selpg。Selpg即Select Pages，允许用户指定从输入文本（可来自文件或命令行或是另一个进程的输出）抽取的页的范围，并控制输出的位置，可以是标准输出，也可以输入至文件或子进程。

Usage

1
2
3
4
5
6
7
8
Usage: selpg [-s startPage] [-e endPage] [-l linesPerPage | -f] [-d printDest] filename

Options:
  -d, --dest string		(Optional) Enter printing destination
  -e, --endPage int		(Mandatory) Input Your endPage
  -f, --pageBreak		(Optional) Choosing pageBreaks mode
  -l, --pageLen int     (Optional) Choosing pageLen mode, enter pageLen
  -s, --startPage int	(Mandatory) Input Your startPage

代码结构

总共有三个函数：

  1. main函数：解析命令参数的入口函数

  2. processArgs函数：处理参数，进行错误处理

  3. processInput函数：经过processArgs函数后，这里根据命令进行（文件）操作

除此之外，还有保存参数的struct：selpgArgs，以及五个解析参数用的flag。

selpgArgs存储内容：

1
2
3
4
5
type selpgArgs struct {
	startPage, endPage, pageLen, pageType int
	inFilename                            string
	printDest                             string
}

关键实现

  • pflag

在前面的参考文章中，可以看到如果使用C语言来解析参数，代码实现还是比较繁杂的，需要手动进行参数的获取、判断乃至解析。而在Go语言中，有很多便利的包供我们使用，在这里使用的是pflag这个包来进行参数的解析。

pflag包的使用是非常简单的，首先go get了这个包(spf13/pflag)之后，引入它就可以使用了。基本的参数绑定操作：

1
2
3
4
5
6
var ip *int = flag.Int("flagname", 1234, "help message for flagname")	//绑定"--flagname"的值到*ip上，格式为int
//或
var flagvar int		//声明
func init() {
    flag.IntVar(&flagvar, "flagname", 1234, "help message for flagname")	//绑定
}

在Selpg中，我们需要两种格式的参数，拿输入文本的起始页做例子，我们就需要同时接受--startPage与-s这两种输入，pflag也允许我们这样做：

1
2
var inputS = flag.IntP("startPage", "s", -1, "...")
//startPage配合"--"使用，s配合"-"使用

最后，flag.Parse()自动进行参数的捕获、解析。如果是没有带-或--的参数，则可通过flag.Args()获取，这类参数的数量为flag.Narg()。

  • bufio

在Selpg的实现中我使用了bufio包来进行输入输出的定向，bufio即buffered I/O，它封装了io.Reader与io.Writer，使用起来还是较为方便的。

读取输入部分：

1
2
3
4
5
6
7
8
9
10
11
12
//从命令行输入
inputReader = bufio.NewReader(os.Stdin) 
//或打开一个文件后输入
file, err = os.Open(selpg.inFilename)
	if err != nil {
		fmt.Fprintln(os.Stderr, err)
		os.Exit(1)
	}
inputReader = bufio.NewReader(file)	
//读取输入，直到某一字符（包含此字符）
line, err = inputReader.ReadBytes('\n')	//换页为行模式
line, err = inputReader.ReadBytes('\f')	//换页为换页符模式

定向输出部分：

1
2
3
outputWriter = bufio.NewWriter(os.Stdout)
outputWriter.Write(line)
outputWriter.Flush()	//这一步必须
  • os/exec

“-dXXX”的实现可能是比较难的一部分，这里通过os/exec包来实现，exec允许运行外部命令，它封装了os.StartProcess，故我们可以更容易地重定向输入输出，可通过管道向命令输入内容。

当-d参数获得了一个打印机地址，就进行如下操作：

1
2
3
4
5
6
7
8
9
//初始化外部命令
cmd = exec.Command("lp", "-d", selpg.printDest)	
//建立一个管道以输入打印内容
stdin, err = cmd.StdinPipe()
//写入管道
_, err := io.WriteString(stdin, string(line))
//关闭管道、获得输出
stdin.Close()
stderr, _ := cmd.CombinedOutput()

注意cmd.CombinedOutput()的作用是运行命令并获得组合在一起的stdout/stderr输出。

简单测试

  • selpg -s1 -e1

即，从命令行输入，并输出到命令行，打印前72行（default）

1

  • selpg -s1 -e1 -l3 input

即，从文件输入，并输出到命令行，打印前三行

2

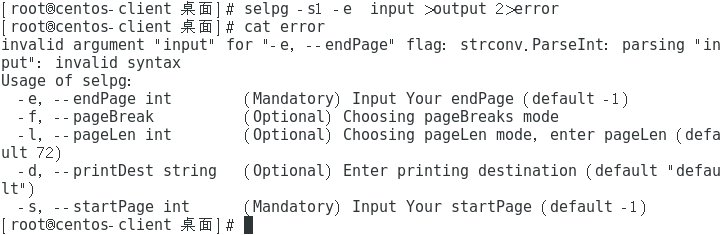
  • selpg -s1 -e input >output 2>error

即，正确输出到文件output，错误输出至文件error（故意写成错误命令）

3

  • 测试换页符，首先建立包含换页符的文件：

4

接着，测试selpg -s1 -e3 -f input

5

  • 测试输出至打印机lp1

6

命令正确执行了，只是没有打印机

  • selpg -s1 -e20 -l20 test.txt | grep -n "Geralt"

测试读取并输出长篇小说的前20页（设置每页长20行）

Geralt

这样就实现了selpg程序。

发表于

题目

There are N rooms and you start in room 0. Each room has a distinct number in 0, 1, 2, ..., N-1, and each room may have some keys to access the next room.

Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, ..., N-1]where N = rooms.length. A key rooms[i][j] = v opens the room with number v.

Initially, all the rooms start locked (except for room 0).

You can walk back and forth between rooms freely.

Return true if and only if you can enter every room.

Example 1:

1
2
3
4
5
6
7
Input: [[1],[2],[3],[]]
Output: true
Explanation:  
We start in room 0, and pick up key 1.
We then go to room 1, and pick up key 2.
We then go to room 2, and pick up key 3.
We then go to room 3.  Since we were able to go to every room, we return true.

Example 2:

1
2
3
Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can't enter the room with number 2.

Note:

  1. 1 <= rooms.length <= 1000
  2. 0 <= rooms[i].length <= 1000
  3. The number of keys in all rooms combined is at most 3000.

解法

总的来说，就是数组的每个位是一个房间，房间中存有通往其他房间的钥匙，从0号房间开始，问是否能走完全部房间。于是马上想到了BFS算法，只要最后所有位置都visit过，就能够走完所有房间。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool canVisitAllRooms(vector<vector<int>>& rooms) {
    vector<int> visited(rooms.size(), 0);	//已到过的房间
    queue<int> tovisit;		//将要去的房间
    tovisit.push(0);
    visited[0] = 1;
    while(!tovisit.empty()){
        int curr = tovisit.front();
        tovisit.pop();
        for(auto r : rooms[curr]){
            if(!visited[r]){
                tovisit.push(r);
                visited[r] = 1;
            }
        }
    }
    for(int i = 0; i < rooms.size(); i++){
        if(!visited[i]){
            return false;
        }
    }
    return true;
}

发表于

国庆长假，水一题

题目

Alex and Lee play a game with piles of stones. There are an even number of piles arranged in a row, and each pile has a positive integer number of stones piles[i].

The objective of the game is to end with the most stones. The total number of stones is odd, so there are no ties.

Alex and Lee take turns, with Alex starting first. Each turn, a player takes the entire pile of stones from either the beginning or the end of the row. This continues until there are no more piles left, at which point the person with the most stones wins.

Assuming Alex and Lee play optimally, return True if and only if Alex wins the game.

Example 1:

1
2
3
4
5
6
7
8
Input: [5,3,4,5]
Output: true
Explanation: 
Alex starts first, and can only take the first 5 or the last 5.
Say he takes the first 5, so that the row becomes [3, 4, 5].
If Lee takes 3, then the board is [4, 5], and Alex takes 5 to win with 10 points.
If Lee takes the last 5, then the board is [3, 4], and Alex takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alex, so we return true.

Note:

  1. 2 <= piles.length <= 500
  2. piles.length is even.
  3. 1 <= piles[i] <= 500
  4. sum(piles) is odd.

解法一

第一种解法是使用动态规划，注意到每次Alex和Lee的操作都是从piles的头或尾取走一个最大的数，那么就可以把问题分解到多个子问题上分别来解决。

先构建一个数组存储piles的备份，以及一个二维数组存储各个子问题的解：

1
2
3
4
5
6
7
8
9
vector<vector<int>> dparr;
vector<int> p;
bool stoneGame(vector<int>& piles) {
    p = piles;
    int size = piles.size();
    vector<vector<int>> tmp(size, vector<int>(size, 0));
    dparr = tmp;
    return dp(0, size - 1) > 0;
}

下面是dp的具体实现，这里将Lee的操作视为从Alex的得分中扣除，最后只要Alex的得分大于零则Alex胜利：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int dp(int low, int high){
    if(low == high){
        return 0;
    }
    if(dparr[low][high] != 0){	//避免重复计算
        return dparr[low][high];
    }
    int res = 0;
    if((high - low + 1) % 2 == 0){  //Alex
        res = max(dp(low + 1, high) + p[low], dp(low, high - 1) + p[high]);
    } 
    else{	//Lee
        res = min(dp(low + 1, high) - p[low], dp(low, high - 1) - p[high]);
    }
    dparr[low][high] = res;
    return res;
}

解法二

让我们回到问题：数组中一共有偶数个元素，Alex先选，Lee后选。那么假设数组有2n个元素，如果Alex第一次选择了元素1，则Lee可以选择2或2n，在之后Alex可以选择3、2n或者2、2n-1，以此类推。也就是说，可以保证Alex一定能够选到所有奇数位置的元素或是所有偶数位置的元素，那么只要一开始知道奇数位置元素之和与偶数位置元素之和哪个更大，就能保证Alex胜利，所以实际上这道题我们只需要：

1
return true;

就能够通过。

发表于 | 更新于

题目

An undirected, connected graph of N nodes (labeled 0, 1, 2, ..., N-1) is given as graph.

graph.length = N, and j != i is in the list graph[i] exactly once, if and only if nodes i and j are connected.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

1
2
3
Input: [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

1
2
3
Input: [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Note:

  1. 1 <= graph.length <= 12
  2. 0 <= graph[i].length < graph.length

解法一

这周刚好学到了BFS、Dijkstra、Bellman–Ford等处理图论问题的算法，这里就能够用上了。这一题是要在无向图中找到经过了每一个节点的最短路径，可以很快想到可以用BFS算法，但是再一想，BFS算法可以用来找两点间最短路径，而这里并没有给出起点和终点，只是单纯的找到一条经过每个节点的最短路径，怎么办呢？

以往使用BFS算法时，是将节点不断加入、弹出队列，在这里我们可以换种思路，比如把从各个节点开始的路径加入、更新、弹出队列，并记录此时路径对应的长度，直到队列为空时，此时经过了所有节点的路径的长度应该被更新了许多次，达到了最小。

首先需要构建一个struct类型，代表此时的路径状态：

1
2
3
4
5
6
7
struct state{
    int visited, tovisit;	//已经过的节点，要访问的节点
    state(int v, int t){
        visited = v;
        tovisit = t;
    }
};

用bits来记录经过的节点：从第n号节点开始即为1 << n = 1...00（n个0），访问完所有节点的路径状态应该是011..1，哪一位为1即代表经过了哪一位，访问节点的邻居后的节点状态这样表示：visited | (1 << neighbour)。

接下来是实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int shortestPathLength(vector<vector<int>>& graph) {
    int n = graph.size();
    queue<state> mqueue;
    vector<vector<int>> dist(1 << n, vector<int>(n, n * n));
    for(int i = 0; i < n; i++){
        mqueue.push(state(1 << i, i));	//queue中一开始设置各个节点开始的初始路径
        dist[1 << i][i] = 0;
    }
    while(!mqueue.empty()){
        state node = mqueue.front();
        mqueue.pop();
        int dis = dist[node.visited][node.tovisit];
        if(node.visited == (1 << n) - 1) return dis;
        for(int neighbour : graph[node.tovisit]){	//通过graph访问节点邻居
            int visited2 = node.visited | (1 << neighbour);
            if(dis + 1 < dist[visited2][neighbour]){	//路径更短则更新
                dist[visited2][neighbour] = dis + 1;
                mqueue.push(state(visited2, neighbour));	//更新后的路径状态再加入queue
            }
        }
    }
}

比较难想到的地方就是对路径状态进行BFS。

解法二

通过官方solution发现了第二种使用了Dynamic Programming的解法，大体上其实和BFS差不多，都是对路径状态进行操作。

解法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int shortestPathLength(vector<vector<int>>& graph) {
    int n = graph.size();
    vector<vector<int>> dist(1 << n, vector<int>(n, n * n));
    for(int i = 0; i < n; i++){
        dist[1 << i][i] = 0;
    }
    for(int visited = 0; visited < 1 << n; ++visited){
        bool repeat = true;
        while(repeat){
            repeat = false;
            for(int tovisit = 0; tovisit < n; ++tovisit){
                int dis = dist[visited][tovisit];
                for(int neighbour : graph[tovisit]){
                    int visited2 = visited | (1 << neighbour);
                    if(dis + 1 < dist[visited2][neighbour]){
                        dist[visited2][neighbour] = dis + 1;
                        if(visited2 == visited) repeat = true;
                    }
                }
            }
        }
    }
    int ans = n * n;
    for(int i : dist[(1 << n) - 1]){
        ans = min(i, ans);
    }
    return ans;
}

可以看到，这种解法是通过多重循环，对dist中每一种路径状态进行更新，最后取都是经过每个节点的路径中最短的一条。

发表于 | 更新于

前情提要

在Win10环境下安装配置VirtualBox，搭建CentOS私有云一节中我们已经成功的配置好了虚拟机上的CentOS私有云，今天就来研究一下GO的开发环境的安装与配置。

安装、配置步骤

1. 安装golang

可以选择在官方下载页处找到最新的版本来下载安装，这里省事起见选择了直接用系统包管理工具安装：

1
# sudo yum install golang

安装完后调用go version命令查看版本号，这里安装的是go 1.9.4

查看go都安装在了哪里：

1
# rpm -ql golang

2. 配置golang环境

go工具为公共代码仓库中维护的开源代码而设计，用go所编写的代码必须放在工作空间内，它包含三个子目录：

  • src目录包含Go的源文件，它们被组织成包（一个目录对应一个包），是运行go install、go run等命令时的当前路径
  • pkg目录包含包对象（golang编译的.a中间文件）
  • bin目录包含可执行文件

创建工作空间目录并设置GOPATH：

1
2
# mkdir $HOME/gowork
# export GOPATH=$HOME/work

并将工作空间中的bin目录添加到PATH中，以便以后直接运行安装的go程序：

1
# export PATH=$PATH:$GOPATH/bin

最后使这些配置生效：

1
# source $HOME/.profile

检查配置可以通过：

1
# go env

3. 安装vscode编辑器与其他

vscode安装

在开始愉快的用go玩耍前还需要安装一款适合你的编辑器，这里选择的是vscode，巨硬大法好嘛。

在官方教程中有展示各个平台的安装流程，在CentOS平台上的安装命令：

1
2
3
4
# sudo rpm --import https://packages.microsoft.com/keys/microsoft.asc
# sudo sh -c 'echo -e "[code]\nname=Visual Studio Code\nbaseurl=https://packages.microsoft.com/yumrepos/vscode\nenabled=1\ngpgcheck=1\ngpgkey=https://packages.microsoft.com/keys/microsoft.asc" > /etc/yum.repos.d/vscode.repo'
# yum check-update	//检查更新
# sudo yum install code

git安装

打开vscode后如果你没有安装git那么它会提醒你安装，如果你之前使用yum命令安装过的话它会提醒你版本太老（CentOS下），所以这里选择手动安装最新版本的git。

首先安装一些后续需要的依赖包：

1
2
# yum install curl-devel expat-devel gettext-devel openssl-devel zlib-devel
# yum install  gcc perl-ExtUtils-MakeMaker

接着如果之前有装过旧版本的话需要卸载：

1
# yum remove git

然后wget下载官方最新版本：

1
2
# wget https://www.kernel.org/pub/software/scm/git/git-2.9.2.tar.gz
# tar -zxvf git-2.9.2.tar.gz

最后，编译安装，配置环境：

1
2
3
4
5
# cd git-2.9.2
# make prefix=/usr/local/git all
# make prefix=/usr/local/git install
# echo "export PATH=$PATH:/usr/local/git/bin" >> /etc/bashrc
# source /etc/bashrc

如果安装出错，应该是还有什么依赖没有安装好，根据提示手动安装就可以。

检查git版本：

1
2
# git version
git version 2.9.2

注意：如果安装完查看版本不是我们安装的最新版，请重新执行下面的操作

1
2
3
# yum remove -y git
# source /etc/bashrc
# git --version

工具包安装

现在总能够开始写go了吧？在vscode创建一个hello.go刚写了条package就发现又报错了，原来是很多golang的tools没有安装，根据vscode的提示一键安装，然而golang.org并不能连上，于是，这一步也要我们手动安装。

首先在go工作空间的src目录下建立一个golang.org文件夹，在其中再建立一个x文件夹，cd切换到x文件夹下，下载插件包：

1
2
# git clone https://github.com/golang/tools.git tools
# git clone https://github.com/golang/lint.git lint

执行完毕后，在x文件夹下会多两个文件夹tools和lint。

最后执行安装命令，安装在vscode中没有安装的工具包，例如：

1
2
3
4
5
# go install golang.org/x/tools/cmd/guru
# go install golang.org/x/tools/cmd/gorename
# go install golang.org/x/tools/cmd/gorename
# go install golang.org\x\lint\golint
...

配置成功！接下来可以使用vs code创建hello.go测试一下：

1
2
3
4
5
6
7
package main

import "fmt"

func main() {
    fmt.Printf("hello, world\n")
}

在终端运行！

1
2
# go run hello.go
hello, world

4. 绑定远程仓库

现在你的go工作空间的架构应该类似这样：

1
2
3
4
5
6
7
8
9
10
bin/
	...                         # 可执行命令
pkg/
	linux_amd64/
		...						# 包对象
src/							#源码
	github.com/
		...
	golang.org/
		...

此时需要在github.com文件夹下创建一个和你自己github账号名称一样的文件夹，这个文件夹作为以后与远程库同步的存放go代码的文件夹，在这个文件夹下可以创建各种包。

在你的github账号上手动创建一个远程库，之后根据提示，在本地文件夹中：

1
2
3
4
5
6
# echo "# xxx" >> README.md
# git init
# git add README.md
# git commit -m "first commit"
# git remote add origin https://github.com/username/xxx.git
# git push -u origin master

之后每次git add、commit后要push时，都要输入自己的账号、密码来操作。当然也可以选择用git ssh，这里就不介绍了。

发表于

自中本聪在2008年于《比特币白皮书》中提出“区块链”概念，并在2009年开发第一个区块即“创世区块”起，十年的时间过去了。在这十年的时间中，区块链技术已有长足的发展，开始初步的进入应用领域、大众视野。而同时，它也面临着许多挑战，这些挑战亟待更多的人来研究、解决。

区块链是借由密码学串接并保护内容的串联交易记录（区块），每个区块包含着前一个区块的加密散列、相应时间戳以及交易数据。它的优点都基于其去中心化的特点，得以在节点无需互相信任的分布式系统中实现基于去中心化信用的点对点交易、协调与协作。举例来说，在现有的中心化信用系统中，交易行为都要通过某个中心化的机构来认证，而在区块链中，认证不是由某一个中心机构进行的，而是记录在每个节点上，是透明化、可追溯的。这样就为解决中心化机构普遍存在的高成本、低效率以及数据存储不安全等问题提供了解决方案。

在优点之外，区块链也面临着许多问题与挑战，这里介绍其中的一部分：

  1. 人才匮乏。目前来说，尽管相应的技术与产业发展的很快，但相关学术研究严重滞后。技术创新缺乏理论支持必然走不远，所以相关领域亟待学术跟进。
  2. 监管问题。以区块链这种去中心化技术搭建的交易平台，在交易过程中，参与者的身份都是匿名的，这就和传统的交易平台完全不同了，传统的监管方式也无法再使用。因此，目前比特币的交易市场中充斥着洗钱、黑市交易的犯罪活动，这些行为如何监管也是需要在未来解决的问题。
  3. 安全问题，这也是区块链迄今为止面临的最重要的问题，如基于PoW共识过程的区块链面临的51%攻击问题，和基于PoS共识过程的区块链面临的N@S攻击问题，更为安全有效的共识机制还需要人们的研究和设计。
  4. 效率。目前完全同步自创世区块至今的区块数据需要大于60gb的存储空间，而这个数字还在持续增加中，即使是部分节点采用轻量化方案，还是不能完全解决此问题。同时，区块链的交易效率非常低，比特币区块链目前每秒仅能处理七笔交易，这就限制了区块链在大多数金融系统高额交易场景中的应用。最后，它的交易确认时间一般为十分钟左右（区块的生成时间），这在小额交易和时间敏感交易中是不可忍受的。

区块链的技术应用可分为三个阶段：

  • 区块链1.0模式：以可编程数字加密货币体系为主要特征。加密货币以比特币、莱特币为代表，具有支付、流通的货币职能。
  • 区块链2.0模式：以可编程金融系统为主要特征。是对金融领域的使用场景和流程进行梳理、优化的应用阶段，以以太坊、瑞波币等为代表的智能合约在这一阶段。
  • 区块链3.0模式：以可编程社会为主要特征，是区块链技术在社会各个领域下的应用场景实现。

需要注意的是，这三个模式并不是演进式发展的，而是并行发展的，在区块链2.0乃至3.0已开始发展的背景下，区块链1.0模式的数字加密货币体系实际上仍远未成熟，还有很长的路要走。

目前部分区块链的项目已初步有了一些简单的应用场景，如通过以太坊网络、BTS平台等发行一些基于区块链技术的项目，但是数量还远远不够，覆盖的应用方向也很少。可以说人们通过比特币认识了区块链，但是区块链技术不仅能够应用于数字加密货币领域，它在数据存储、鉴证，金融交易，资产管理和选举投票等方面都有广大的应用前景。总的来说，区块链技术目前还在积累阶段，它的潜力是巨大的，也许，在未来它不仅能改变我们的交易方式，还能深入的影响我们社会的方方面面，甚至，改变整个社会。

发表于

这周因为两道题目都只想到了一种解法，所以写在一起。

1. Swim In Rising Water

On an N x N grid, each square grid[i][j] represents the elevation at that point (i,j).

Now rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distance in zero time. Of course, you must stay within the boundaries of the grid during your swim.

You start at the top left square (0, 0). What is the least time until you can reach the bottom right square (N-1, N-1)?

Example 1:

1
2
3
4
5
6
7
8
Input: [[0,2],[1,3]]
Output: 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.

You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
Input: [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation:
 0  1  2  3  4
24 23 22 21  5
12 13 14 15 16
11 17 18 19 20
10  9  8  7  6

The final route is marked in bold.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.

Note:

  1. 2 <= N <= 50.
  2. grid[i][j] is a permutation of [0, …, N*N - 1].

解法

这道题的意思是，在t时刻，海拔为t，而n*n的二维矩阵的每个数值都代表了一处的海拔，从一点游到另一点的条件是两处的海拔（值）都大于等于t，要求求出从（0，0）到（n-1，n-1）的最小时间。也就是一个搜索节点的问题，可以用bfs即广度优先搜索的思路来做。

在寻找足够大的t时，我用二分法来实现，这样又可以节约不少时间：

1
2
3
4
5
6
7
8
9
10
11
int swimInWater(vector<vector<int>>& grid) {
    int n = grid.size(), st = grid[0][0], ed = n * n - 1, t = 0;
    while(st < ed){
        t = (st + ed) / 2;
        if(swim(grid, t)){	//判断t时能否到达终点
            ed = t;
        }
        else st = t + (st + ed) % 2;
    }
    return st;
}

真正的实现函数里，bfs用一个queue来实现，还要一个二维vector来记录已经到过的节点。然后就是每次把和节点相邻的未经过的节点（且是数值小于等于t的）加入bfs，并把现有节点pop出去，看能否在bfs为空之前找到终点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool swim(vector<vector<int>>& grid, int t){
    int n = grid.size();
    queue<pair<int, int>> bfs;
    vector<vector<int>> visited(n, vector<int>(n));
    int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};	//右左下上
    bfs.emplace(0, 0);
    visited[0][0] = 1;
    while(bfs.size()){
        int x = bfs.front().first, y = bfs.front().second;
        bfs.pop();
        if(grid[x][y] <= t){
            if(x == n - 1 && y == n - 1) return true;
            for(auto d : dir){
                int xs = x + d[0], ys = y + d[1];
                if(xs >= 0 && xs < n && ys >= 0 && ys < n && !visited[xs][ys]){	//判断边界
                    visited[xs][ys] = 1;
                    bfs.emplace(xs, ys);
                }
            }
        }
    }
    return false;
}

这样就完成了这一道题。

2. Couples Holding Hands

N couples sit in 2N seats arranged in a row and want to hold hands. We want to know the minimum number of swaps so that every couple is sitting side by side. A swap consists of choosing any two people, then they stand up and switch seats.

The people and seats are represented by an integer from 0 to 2N-1, the couples are numbered in order, the first couple being (0, 1), the second couple being (2, 3), and so on with the last couple being (2N-2, 2N-1).

The couples’ initial seating is given by row[i] being the value of the person who is initially sitting in the i-th seat.

Example 1:

1
2
3
Input: row = [0, 2, 1, 3]
Output: 1
Explanation: We only need to swap the second (row[1]) and third (row[2]) person.

Example 2:

1
2
3
Input: row = [3, 2, 0, 1]
Output: 0
Explanation: All couples are already seated side by side.

Note:

  1. len(row) is even and in the range of [4, 60].
  2. row is guaranteed to be a permutation of 0...len(row)-1.

解法（伪）

在这道题目中，有许多对couple，他们是(0, 1), (2, 3), …, (2n-2, 2n-1)。现在它们的顺序被打乱了，而你可以随即调换元素的位置，你需要找到调换次数最少的方案。

我的做法是简单的在判断两个元素不是一对couple后，往后查找它的couple并替换，同时调换次数增加一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int minSwapsCouples(vector<int>& row) {
    int swap = 0;
    for(int i = 0; i < row.size() - 1; i += 2){
        if(row[i] % 2){
            if(row[i + 1] != row[i] - 1){
                swap++;
                for(int j = i + 2; j < row.size(); j++){
                    if(row[j] == row[i] - 1){
                        int temp = row[j];
                        row[j] = row[i + 1];
                        row[i + 1] = temp;
                        break;
                    }
                }
            }
        }
        else{
            if(row[i + 1] != row[i] + 1){
                swap++;
                for(int j = i + 2; j < row.size(); j++){
                    if(row[j] == row[i] + 1){
                        int temp = row[j];
                        row[j] = row[i + 1];
                        row[i + 1] = temp;
                        break;
                    }
                }
            }
        }
    }
    return swap;
}

你以为这样就结束了吗？

cyclic swapping

上面的解法是在循环中嵌套一个循环，效果显然是不行的，通过leetcode的discuss，我学到了一种更为优秀的解法：cyclic swapping。

这个解法的精华在于：i == ptn[pos[ptn[row[i]]]]，乍一看确实毫无头绪，但要首先了解两个额外设置的数组ptn和pos：

  1. ptn[i]指的是标签i的couple的值（i可以是位置也可以是具体的值）—— 若i为偶数，ptn[i] = i + 1，若i为奇数，ptn[i] = i - 1。
  2. pos[i]指的是标签i在row数组（也就是给定的随机数组）中的index —— row[pos[i]] == i。

这样一来，i == ptn[pos[ptn[row[i]]]]的意思就是：

  1. 在位置i上的元素有值row[i]，我们想把它放在它couple的旁边。
  2. 首先找到它的couple的值，也就是ptn[row[i]]。
  3. 接着找到这个couple的位置，也就是pos[ptn[row[i]]]。
  4. 最后找到这个位置旁的位置，也就是ptn[pos[ptn[row[i]]]]。

接着就可以进行调换了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int minSwapsCouples(vector<int>& row) {
    int res = 0, N = row.size();
    vector<int> ptn(N, 0);
    vector<int> pos(N, 0);
    for (int i = 0; i < N; i++) {
        ptn[i] = (i % 2 == 0 ? i + 1 : i - 1);
        pos[row[i]] = i;
    }//初始化
    
    for (int i = 0; i < N; i++) {
        for (int j = ptn[pos[ptn[row[i]]]]; i != j; j = ptn[pos[ptn[row[i]]]]) {
            swap(row[i], row[j]);
            swap(pos[row[i]], pos[row[j]]);
            res++;	//调换次数
        }	//这里的循环实际上只是完成一个位置的调换，如果这里的循环多于一次，后面的循环次数会减少
    }
        
    return res;
}

发表于 | 更新于

题目

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

  • Integers in each row are sorted in ascending from left to right.
  • Integers in each column are sorted in ascending from top to bottom.

Example:

Consider the following matrix:

1
2
3
4
5
6
7
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.

Given target = 20, return false.

解法一

拿到题目一看是查询类的，先暴力解了再说，解法就是两层循环遍历找到值。实现如下：

1
2
3
4
5
6
7
8
9
10
11
bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if(matrix.empty() || matrix[0].empty()) return false;
    for(int i = 0; i < matrix.size(); i++){
        for(int j = 0; j < matrix[i].size(); j++){
            if(matrix[i][j] == target){
                return true;
            }
        }
    }
    return false;
}

容易看出，这样做的复杂度达到了O(m*n)（m、n对应矩阵的行和列），肯定是不能够让人满意的。

解法二

接下来有哪些地方可以改进的呢？注意这个二维矩阵，暴力求解的时候对每一行是直接顺序扫描，那么这里可以改成对一行进行二分查找，这样一来复杂度可以减少到O(m*logn)，实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
bool bisearch(vector<int>& line, int head, int tail, int target){
    int mid = line[(head + tail) / 2];
    if(head == tail){
        return mid == target;
    }
    if(mid == target){
        return true;
    }
    if(mid < target){
        return bisearch(line, (head + tail) / 2 + 1, tail, target);
    }
    else{
        return bisearch(line, head, (head + tail) / 2, target);
    }
}
bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if(matrix.empty() || matrix[0].empty()) return false;
    for(int i = 0; i < matrix.size(); i++){
        if(matrix[i].size() == 1 && matrix[i][0] == target){
            return true;
        }
        else{
            if(target > matrix[i][matrix[i].size() - 1]) continue;
            if(target < matrix[i][0]) return false;
            if(bisearch(matrix[i], 0, matrix[i].size() - 1, target)){
                return true;
            }
        }
    }
    return false;
}

解法三

按照上一个解法提交后我发现成绩还是不尽人意（运行时间在所有成功提交中在中间的位置），那么还能怎么改进呢？思考了许久后，我发现是自己一开始就陷入思维定势了，因为这道题类型属于divide and conquer，所以就一直想着二分，其实并不一定要这么做。

重点是要分析透彻这个矩阵的特点，它的每一行、列的元素都是按从小到大的顺序排列好的，所以每个元素的左边元素都比它小，下面元素都比它大，那么只需要从第一行最右元素开始比较，若比target小就向下移动一位（这一行剩下的不需要查找了），若比target大就向左移动一位，这样若矩阵中存在target那么肯定能够找到。其实从最后一行第一个元素开始也可以，原理是一样的。

实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if(matrix.empty() || matrix[0].empty()) return false;
    int i = 0, j = matrix[0].size() - 1;
    while(j >= 0 && i < matrix.size()){
        if(matrix[i][j] == target){
            return true;
        }
        else if(matrix[i][j] > target){
            j--;
        }
        else{
            i++;
        }
    }
    return false;
}

值得一提的是，这样完成的复杂度最差情况下为O(m+n)。