友情链接：

1. Win10环境下搭建Ubuntu私有云
2. MAC环境下搭建Ubuntu私有云

（同队队员的博客，给有需要在windows、mac环境下搭建Ubuntu虚拟机的同学）

准备工作

1. 安装VirtualBox，根据自己的需要下载相应的host版本，在这里我下载的是VirtualBox 5.2.18的Windows host版，下载地址：官网
2. 安装Git客户端（git bash），下载地址：官网
3. 下载Linux发行版镜像，可以选择在阿里云opsx进行下载，在这里我选择的是CentOS7镜像进行下载。

配置VirtualBox

在创建安装虚拟机之前，要先配置虚拟机的存储位置，避免占用不必要的空间。

• VirtualBox菜单：管理 → 全局设定 → 常规 → 默认虚拟电脑位置

之后要创建虚拟机内部虚拟网络，是将来用来测试虚拟机与主机间通讯时要用到的。

• VirtualBox菜单：管理 → 主机网络管理器

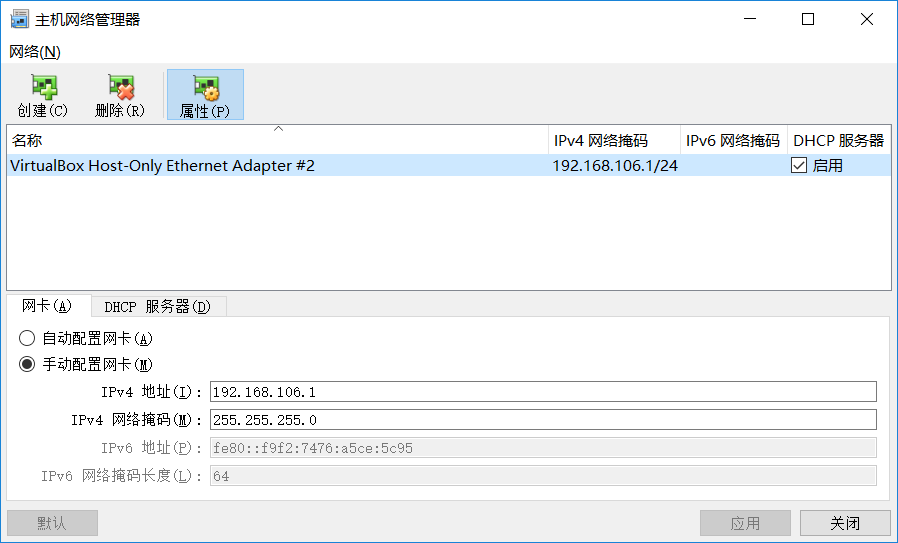
将网卡改为手动配置，自行修改Ipv4地址，注意这个地址是作为虚拟内部网络host的地址，后续虚拟机的ip地址不能与之相同。

配置界面：

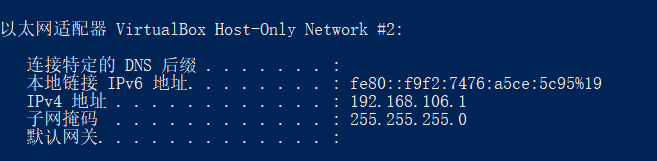
配置网络完成后，在主机windows命令行输入ipconfig，可以看到我们创建的网卡的信息。

配置CentOS虚拟机

首先用vbox创建一个64 bit虚拟机，命名为centos-base，以便与后面另外创建的虚拟机区分。因为对于这个虚拟机计划只使用命令行操作，所以CPU、内存、显存都采用默认配置就可以，存储设置为30G，避免以后扩展麻烦。

比较重要的是网络的配置：

• 设置 → 网络

第一块网卡设置为NAT（不用调整），这块网卡负责访问外网（通过宿主机）。第二块网卡连接方式：Host-Only，接口为之前创建的虚拟网卡VirtualBox Host-Only Ethernet Adapter #2，这块网卡负责进行虚拟网络连接。

之后导入之前下载的iso文件进行系统安装，完成后进入系统。

进入系统后，第一件事要升级OS系统内核：

• 首先获取wget，yum install wget

• 系统自带的源可能比较慢，可以换成163或阿里云的源，这里选择163源进行更换：

  • 首先备份/etc/yum.repos.d/CentOS-Base.repo

    mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup

  • 下载对应版本repo文件（这里为CentOS7），并放入/etc/yum.repos.d

    wget http://mirrors.163.com/.help/CentOS7-Base-163.repo

  • 运行以下命令生成缓存

    yum clean all

    yum makecache

• 最后 yum update

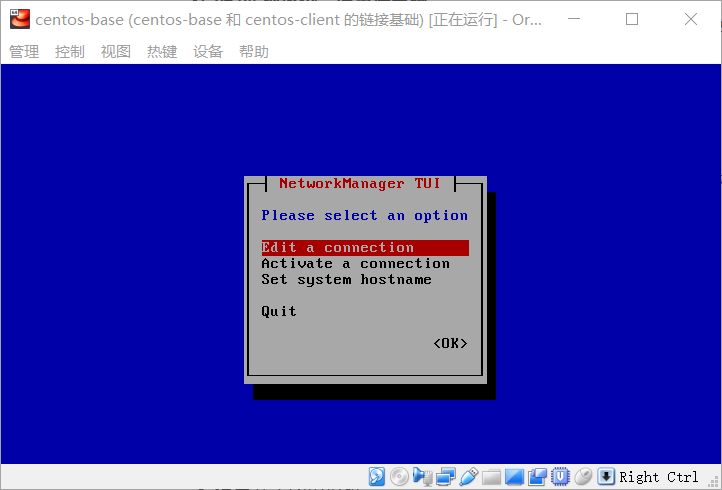
接着检查网卡配置，命令行输入nmtui，出现配置网卡的界面：

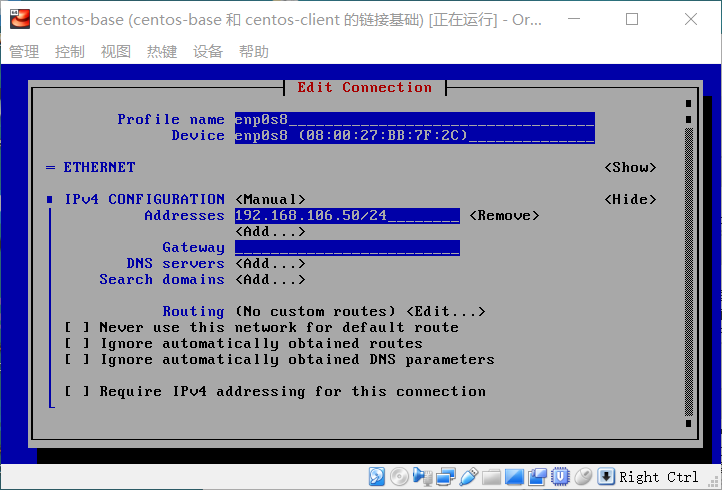
进入Edit之后可以看到有enp0s8、enp0s3两个以太网连接，分别对应刚才的Host-Only和NAT。对于enp0s3不用如何调整，只需要在enp0s8的edit界面设置ipv4地址：

设置好了不要忘记在activate界面手动激活网卡，因为这里默认开机时不会启动网卡。当然，也可以设置它开机时自动启动。找到网卡的配置文件（在/etc/sysconfig/network-scripts中），将ifcfg-enp0s8和ifcfg-enp0s3（名称对应你的网卡名称）中的ONBOOT选项都改为true，这样就能开机自启了。

接下来尝试ping外网与内网：

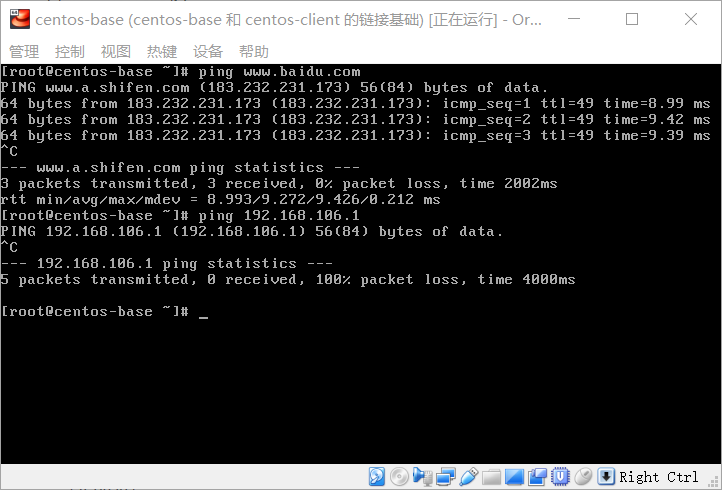
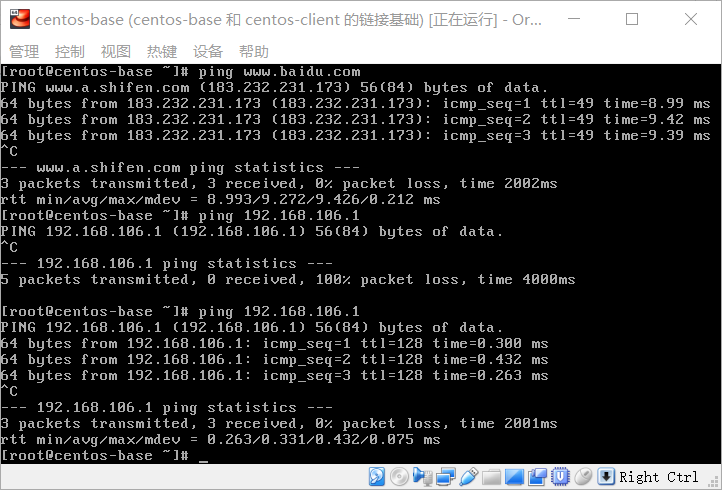
咦，为什么内网无法ping到？网卡的设置应该是没有问题的，同时我试了一下在windows这边命令行ping 192.168.106.50，也就是虚拟机地址，是没有问题的，说明应该是有一个协议使得连接只能是单向的了，那就应该是windows防火墙的问题了，win10防火墙有三种：域网络、专用网络和公共网络。关闭win10的专用网络防火墙后，果然可以了：

下面开始配置第二个CentOS虚拟机，这个虚拟机只需要对centos-base进行复制就可以了，这里把新的虚拟机命名为centos-client，注意复制选项，必须选择重新初始化所有网卡的MAC地址，不然后面无法测试虚拟机之间的通信（地址相同）。最后选择链接复制，此时新虚拟机的虚拟硬盘是绑定到原虚拟机的虚拟硬盘的，这样虚拟机创建的就很快。

同样，在第二个虚拟机中，用nmtui配置主机名与第二块网卡的地址，并测试能否ping通，测试结果都很正常。

在这个虚拟机中打算使用centos 桌面，故分配给它的CPU、内存与显存都要调高一些，并使用yum groupinstall "GNOME Desktop"来安装桌面，安装成功后，设置启动目标为桌面：ln -sf /lib/systemd/system/runlevel5.target /etc/systemd/system/default.target，再重启，就可以看到centos桌面了：

ssh与远程桌面访问

既然是建立私有云，用ssh和远程桌面访问是必不可少的。而要使用这两个工具也需要做一些工作。

首先对于ssh：

• 确保CentOS7安装了openssh-server，在终端输入yum list installed | grep openssh-server

• 如果显示没有安装，就输入yum install openssh-server来安装

• 有了openssh-server后，找到/etc/ssh/目录下的sshd_config文件并用编辑器打开，将Port、ListenAddress前的＃号去除，并把PermitRootLogin和PasswordAuthentication设为yes

  

  

  

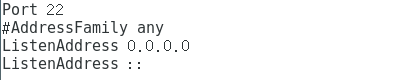
测试ssh连接成功：

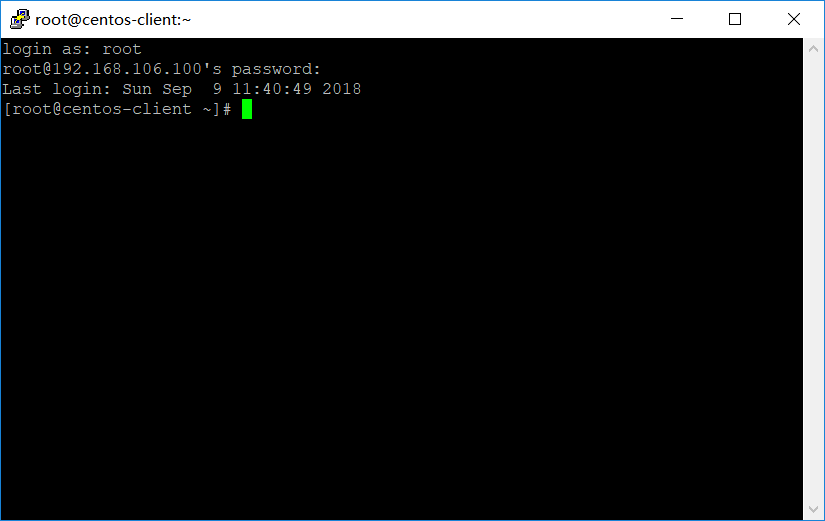
接下来是远程桌面访问：

• 首先要安装VirtualBox远程显示系统的扩展包Oracle VM VirtualBox Extension pack，它提供一系列的功能支持：USB 2.0，intel网卡的PXE启动与VirtualBox远程显示系统。安装完成后，重启宿主机。

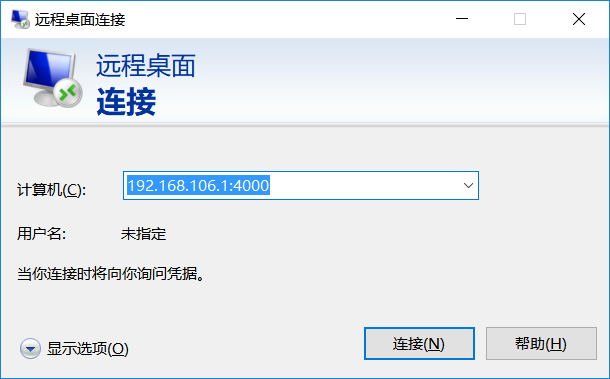
• 设置虚拟机访问端口：点击虚拟机设置 → 显示 → 远程桌面 → 启用服务器并设置连接端口，注意连接时用的是宿主机的IP地址加上子机的端口（也就是192.168.106.1:（设置的端口）），每台虚拟机必须拥有唯一的RDP访问端口。

• 最后，用Windows的Remote Desktop Connection（远程桌面连接）终端进行远程桌面访问（注意先启动虚拟机）

  

  

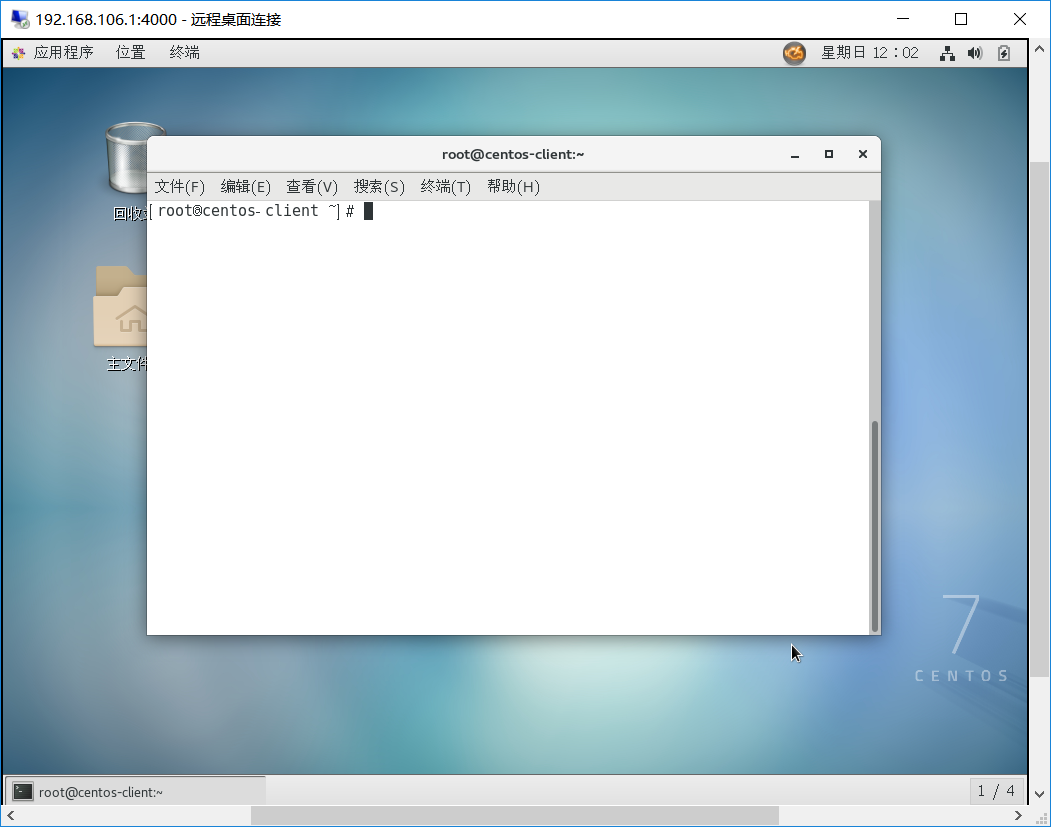
这样以来，私有云就搭建好了，可以开始愉快的玩耍了~

最近准备参加CCF认证，刷一下这里的题目。

题目

问题描述

数轴上有一条长度为L（L为偶数)的线段，左端点在原点，右端点在坐标L处。有n个不计体积的小球在线段上，开始时所有的小球都处在偶数坐标上，速度方向向右，速度大小为1单位长度每秒。

当小球到达线段的端点（左端点或右端点）的时候，会立即向相反的方向移动，速度大小仍然为原来大小。

当两个小球撞到一起的时候，两个小球会分别向与自己原来移动的方向相反的方向，以原来的速度大小继续移动。

现在，告诉你线段的长度L，小球数量n，以及n个小球的初始位置，请你计算t秒之后，各个小球的位置。

提示

因为所有小球的初始位置都为偶数，而且线段的长度为偶数，可以证明，不会有三个小球同时相撞，小球到达线段端点以及小球之间的碰撞时刻均为整数。

同时也可以证明两个小球发生碰撞的位置一定是整数（但不一定是偶数）。

输入格式

输入的第一行包含三个整数n, L, t，用空格分隔，分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。

第二行包含n个整数a1, a2, …, an，用空格分隔，表示初始时刻n个小球的位置。

输出格式

输出一行包含n个整数，用空格分隔，第i个整数代表初始时刻位于ai的小球，在t秒之后的位置。

Example :

1
2
3

Input: 3 10 5
	   4 6 8
Output: 7 9 9

题解

一开始可能有点懵，不过想到每个小球都有自己的运动方向、位置，就可以联想到建立对象来解题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

int length;	//每个球都再判断是否碰墙的时候都需要这个值
class Ball{
    public:
        Ball(){
            direction = 1;
            this->pos = 0;
        }
        int getpos(){
            return pos;
        }
        void initpos(int pos){
            this->pos = pos;
        }
        void move(){
            pos = (direction) ? pos + 1 : pos - 1;
        }
        bool againstwall(){
            return (pos == 0 || pos == length) ? true : false;
        }
        void turn(){
            direction = (direction == 1) ? 0 : 1;
        }
    private:
        int pos;
        int direction;
};

类建好后，解题就比较简单了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

int main(){
    int numofball, time;
    cin >> numofball >> length >> time;
    Ball *balls = new Ball[numofball];
    for(int i = 0; i < numofball; i++){
        int pos;
        cin >> pos;
        balls[i].initpos(pos);
    }
    while(time--){
        for(int i = 0; i < numofball; i++){
            balls[i].move();
            if(balls[i].againstwall()){
                balls[i].turn();
            }
        }
        for(int i = 0; i < numofball - 1; i++){
            for(int j = i + 1; j < numofball; j++){
                if(balls[i].getpos() == balls[j].getpos()){
                    balls[i].turn();
                    balls[j].turn();
                    break;
                }
            }
        }
    }
    for(int i = 0; i < numofball; i++){
        cout << balls[i].getpos() << " ";
    }
    cout << endl;
    return 0;
}

这里球跟球之间的碰撞处理的比较简单粗暴，不过暂时也没有想到更好的方法（其实是懒），就先这样吧。

题目

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

1
2
3

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

1
2

Input: "cbbd"
Output: "bb"

解法一

首先想到的当然是暴力解法了，对字符串的每一子字符串都进行是否为回文字符串的判定。所谓回文字符串就是正反都一样的字符串。

解法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

bool isPalindrome(string s){
    for(int i = 0; i < s.length() / 2; i++){
        if(s[i] != s[s.length() - 1 - i]){
            return false;
        }
    }
    return true;
}
string longestPalindrome(string s) {
    int maxlength = 1;
    string longeststr = s.substr(0, 1);
    for(int i = 0; i < s.length(); i++){
        if(maxlength >= s.length() - i) return longeststr;
        for(int j = maxlength + 1; j <= s.length() - i; j++){
            if(isPalindrome(s.substr(i, j))){
                if(j > maxlength){
                    longeststr = s.substr(i, j);
                    maxlength = j;
                }
            }
        }
    }
    return longeststr;
}

这里也对暴力解法进行了一些优化，比如在外层循环时，如果已经得到的最长回文字符串的长度大于此时要处理的子字符串的长度就直接返回；内存循环直接从此时得到的最长回文字符串的长度+1开始。然而，可以想见的是，效果依然是很差的。

解法二

之后思考许久也没有找到更好的算法，遂查看leetcode的提示，提示是说在寻找新的更长的回文字符串时，要用到已计算的回文字符串。这样一来可以减少判断回文字符串的时间。

解法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

string longestPalindrome(string s) {
    int minstart = 0, maxlength = 1;
    for(int i = 0; i < s.size(); i++){
        int sub = i, add = i;
        while(add < s.size() - 1 && s[add + 1] == s[add]){
            add++;
        }
        while(sub > 0 && add < s.size() - 1 && s[add + 1] == s[sub - 1]){
            add++;
            sub--;
        }
        int newlength = add - sub + 1;
        if(newlength > maxlength){
            minstart = sub;
            maxlength = newlength;
        }
    }
    return s.substr(minstart, maxlength);
}

这个解法是每次以循环位置i为中心，向两端扩展找到最长的回文字符串，在判断是否为回文字符串时，实际上只用判断s[add + 1] == s[sub - 1]，也就是这一步时间复杂度仅为O(1)，这样就大幅缩短了算法运行的时间。